Complexity Models

1. Giới thiệu về Độ phức tạp thuật toán

Độ phức tạp tính toán đo lường số lượng các thao tác cơ bản (cộng, nhân, đọc, ghi, …) được thực hiện trong một thuật toán.
Được hình thành từ những năm 1960 và trở thành một mô hình chuẩn để đánh giá hiệu suất thuật toán.
Mô hình này phản ánh cách máy tính hoạt động vào thời điểm đó.

2. Lý thuyết độ phức tạp cổ điển

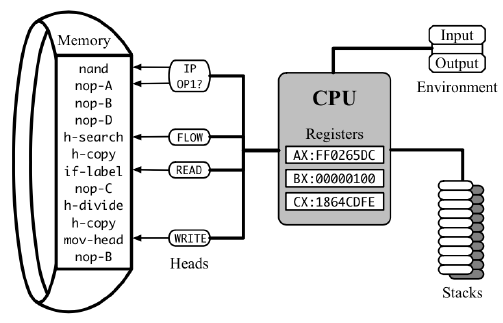
Bộ xử lý (CPU) thực thi chương trình dưới dạng các lệnh (instructions), mỗi lệnh có độ trễ (latency) khác nhau.
CPU có con trỏ lệnh (instruction pointer) để xác định lệnh tiếp theo cần thực thi.
Tổng thời gian chạy chương trình được tính bằng tổng độ trễ của các lệnh chia cho tần số xung nhịp (clock frequency).

Ví dụ về phép nhân ma trận:

Nhân hai ma trận n×n cần khoảng: n³ phép nhân và n²(n-1) phép cộng.
Tra cứu độ trễ:
- Phép nhân: 3 chu kỳ.
- Phép cộng: 1 chu kỳ.
- Tổng số chu kỳ cần: 4n³−3n²

Lưu ý: Thời gian thực thi còn phụ thuộc vào nhiệt độ CPU, hệ điều hành, mức tiêu thụ điện năng của các linh kiện khác.

3. Độ phức tạp tiệm cận (Asymptotic Complexity)

Ý tưởng chính: Biểu diễn thời gian chạy như một hàm theo kích thước đầu vào.
Trong những năm 1960, máy tính rất đắt và chậm nên người ta quan tâm đến bài toán hữu hạn hơn là tính toán trên tập dữ liệu lớn.
Khi máy tính phát triển nhanh, người ta bỏ qua hằng số và chỉ quan tâm đến bậc lớn nhất trong hàm độ phức tạp.
- Ví dụ: 4n³−3n² được viết đơn giản thành O(n³).

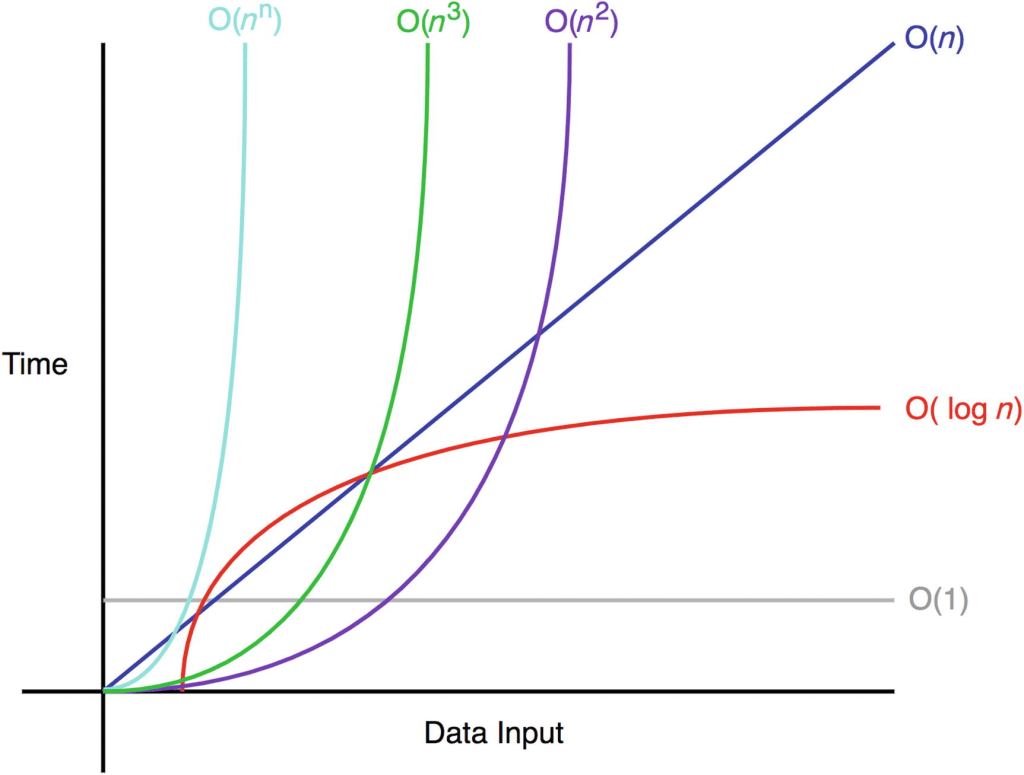
Vì sao dùng độ phức tạp tiệm cận?

Giúp đơn giản hóa đánh giá thuật toán trong trường hợp dữ liệu lớn.
Bỏ qua chi tiết phần cứng và tập trung vào bản chất thuật toán.
So sánh trực quan giữa các thuật toán.

Nhưng tại sao cách tiếp cận này không hoàn toàn đúng?

Sự phát triển về tốc độ xử lý không còn phụ thuộc hoàn toàn vào xung nhịp CPU.
Những yếu tố như kiến trúc vi xử lý, bộ nhớ cache, song song hóa ảnh hưởng lớn đến thời gian chạy thực tế.

4. Kết luận

Độ phức tạp thuật toán là một công cụ hữu ích để phân tích thuật toán nhưng không phản ánh hoàn toàn tốc độ thực tế.
Các mô hình độ phức tạp tiệm cận (Big O, Theta, Omega) giúp so sánh thuật toán trên tập dữ liệu lớn.
Tuy nhiên, để tối ưu hóa thuật toán cho hệ thống thực tế, cần xem xét các yếu tố phần cứng và tối ưu hóa cấp độ vi xử lý.

Tóm lại, tài liệu này cung cấp một cái nhìn tổng quan về độ phức tạp thuật toán từ lý thuyết cổ điển đến cách tiếp cận tiệm cận hiện đại, đồng thời nhấn mạnh giới hạn của các mô hình độ phức tạp truyền thống khi áp dụng vào thực tế.