Algorithms for Modern Hardware
- Part I: Performance Engineering
Nếu bạn từng mở một quyển sách giáo trình khoa học máy tính, có lẽ nó đã giới thiệu về tính phức tạp tính toán (computational complexity) ở đâu đó từ đầu. Đơn giản là, đó là tổng số lần thực hiện các phép toán cơ bản (cộng, nhân, đọc, ghi…) trong quá trình tính toán, có thể được đánh trọng số bởi chi phí tương ứng.
Khái niệm về độ phức tạp là một khái niệm cũ. Nó đã được hình thành một cách có hệ thống vào đầu những năm 1960 và từ đó đã được sử dụng rộng rãi như một hàm chi phí để thiết kế thuật toán. Lý do mà mô hình này được chấp nhận nhanh chóng là vì nó là một ước lượng tốt về cách máy tính hoạt động vào thời điểm đó.
Lý Thuyết Độ Phức Tạp Cổ Điển (Classical Complexity Theory)
Những “phép toán cơ bản” (elementary operations) của một CPU được gọi là các lệnh (instructions), và “chi phí” (costs) của chúng được gọi là độ trễ (latencies). Các lệnh được lưu trữ trong bộ nhớ (memory) và được thực hiện từng lệnh một bởi bộ xử lý (processor), có một trạng thái nội tại (internal state) được lưu trữ trong một số thanh ghi (registers). Một trong những thanh ghi này là con trỏ lệnh (instruction pointer), chỉ định địa chỉ của lệnh tiếp theo cần đọc và thực hiện. Mỗi lệnh thay đổi trạng thái của bộ xử lý theo một cách nhất định (bao gồm việc di chuyển con trỏ lệnh), có thể sửa đổi bộ nhớ chính (main memory) và mất một số chu kỳ CPU (cycles) khác nhau để hoàn thành trước khi lệnh tiếp theo có thể bắt đầu.
Để ước lượng thời gian chạy thực tế của một chương trình, bạn cần tổng tất cả các độ trễ cho các lệnh đã thực hiện của nó và chia cho tần số xung đồng hồ (clock frequency), tức là số chu kỳ mà một CPU cụ thể thực hiện mỗi giây.

Tần số xung đồng hồ là một biến thay đổi và thường không biết trước, phụ thuộc vào mô hình CPU, cài đặt hệ thống, nhiệt độ hiện tại của vi mạch, việc sử dụng điện của các thành phần khác và một số yếu tố khác. Ngược lại, độ trễ của lệnh là các giá trị cố định và thậm chí khá nhất quán trên các CPU khác nhau khi được biểu thị trong chu kỳ đồng hồ, vì vậy việc đếm chúng thay vì tần số xung đồng hồ là rất hữu ích cho mục đích phân tích.
Ví dụ, thuật toán nhân ma trận theo định nghĩa yêu cầu tổng cộng n2⋅(n+n−1) phép toán số học: cụ thể, n3 lần nhân và n2⋅(n – 1) lần cộng. Nếu chúng ta tra cứu độ trễ cho những lệnh này (trong các tài liệu đặc biệt được gọi là bảng lệnh (instruction tables), như ví dụ này), chúng ta có thể tìm thấy rằng, ví dụ, phép nhân mất 3 chu kỳ, trong khi phép cộng mất 1 chu kỳ, vì vậy chúng ta cần tổng cộng 3⋅n3+n2⋅(n−1)=4⋅n3−n2 chu kỳ đồng hồ cho toàn bộ quá trình tính toán (mà không để ý đến những gì cần phải làm để “cung cấp” các lệnh này với dữ liệu đúng).
Tương tự như cách tổng của độ trễ lệnh có thể được sử dụng như một chỉ số không phụ thuộc vào đồng hồ để đánh giá thời gian thực hiện tổng cộng, độ phức tạp tính toán có thể được sử dụng để đánh giá yêu cầu thời gian cố định của một thuật toán trừu tượng, mà không phụ thuộc vào việc chọn lựa máy tính cụ thể.
Độ Phức Tạp Tiệm Cận (Asymptotic Complexity)
Ý tưởng biểu diễn thời gian thực hiện như một hàm của kích thước đầu vào có vẻ rõ ràng ngày nay, nhưng không hẳn như vậy vào những năm 1960. Lúc đó, máy tính phổ thông có giá hàng triệu đô la, cỡ lớn đến mức cần một phòng riêng biệt và tần số xung đồng hồ được đo bằng kilôhertz. Chúng được sử dụng cho các nhiệm vụ thực tế như dự đoán thời tiết, phóng tên lửa vào không gian hoặc xác định xem một tên lửa hạt nhân của Liên Xô có thể đi xa bao xa từ bờ biển của Cuba — tất cả đều là các vấn đề có chiều dài hữu hạn. Các kỹ sư thời kỳ đó chủ yếu quan tâm đến cách nhân ma trận 3 x 3 thay vì những ma trận n x n.
Điều làm thay đổi mọi thứ là sự tự tin giữa các nhà khoa học máy tính rằng máy tính sẽ tiếp tục trở nên nhanh hơn — và thực sự chúng đã làm được điều đó. Theo thời gian, người ta dừng việc đếm thời gian thực hiện, sau đó dừng việc đếm chu kỳ, và thậm chí dừng việc đếm chính xác số phép toán, thay vào đó là một ước lượng chỉ sai lệch bằng một hằng số trên các đầu vào đủ lớn. Với độ phức tạp tiệm cận, chuỗi chi tiết “4⋅n 3 −n 2 phép toán” biến thành “Θ(n 3 ),” che giấu đi chi phí ban đầu của từng phép toán riêng lẻ trong “Big O,” cùng với tất cả các chi tiết phức tạp của phần cứng khác.
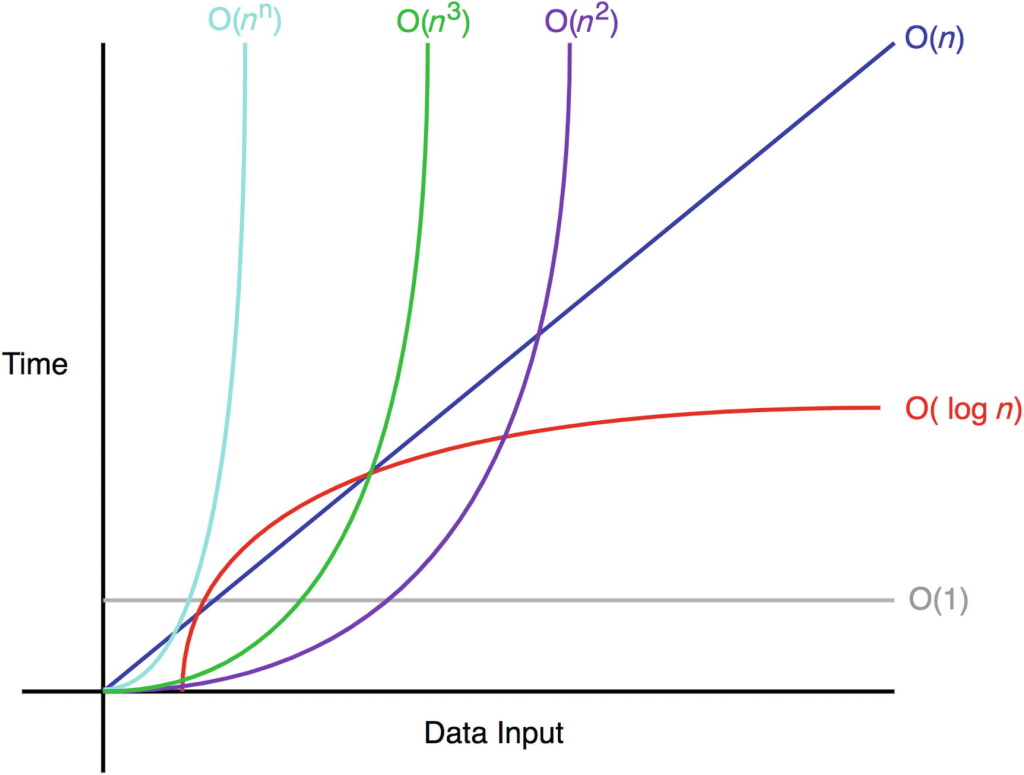
Lý do chúng ta sử dụng độ phức tạp tiệm cận là vì nó mang lại sự đơn giản mà vẫn đủ chính xác để đưa ra kết quả hữu ích về hiệu suất tương đối của thuật toán trên tập dữ liệu lớn. Dưới sự hứa hẹn rằng máy tính sẽ cuối cùng trở nên đủ nhanh để xử lý bất kỳ đầu vào đủ lớn nào trong một khoảng thời gian hợp lý, các thuật toán tiệm cận nhanh hơn luôn sẽ nhanh hơn trong thời gian thực, bất kể hằng số ẩn.
Tuy nhiên, hứa hẹn này cuối cùng không trở thành sự thật — ít nhất không đúng với tần số xung đồng hồ và độ trễ của các lệnh — và trong chương này, chúng tôi sẽ cố gắng giải thích tại sao và cách làm thế nào để đối mặt với điều này.